This post originally appeared on Business Insider.
The question of how to win at rock-paper-scissors has, believe it or not, plagued mathematicians and game theorists for quite some time. While they previously had devised a theoretical answer to the question, a new experiment by Zhijian Wang at Zhejiang University in China that used real players, has revealed an interesting wrinkle to the original theory.
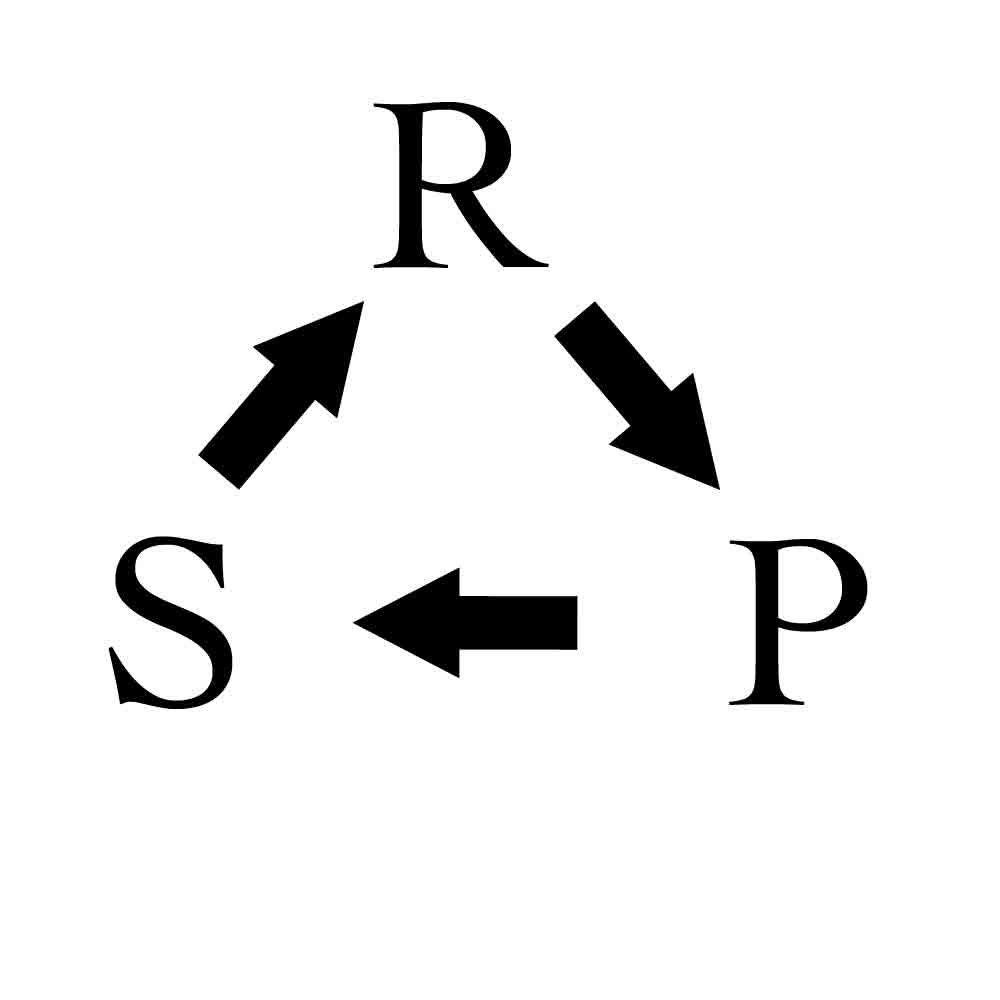
In the experiment, Wang noticed that winning players tended to stick with their winning strategy, while losers tended to switch to the next strategy in the sequence of rock-paper-scissors, following what he calls, “persistent cyclic flows.”
Here’s how it works in practice: Player A and Player B both start by using random strategies. If Player A uses rock and Player B uses paper, Player A loses. In the next round, Player A can assume that Player B will use paper again and should therefore use scissors to win. In the round after that, because Player B lost, Player A can assume that Player B will use the next strategy in the sequence—scissors—and Player A should then use rock, thus winning again.
If you take the game on a theoretical level, the most mathematically sound way to play rock-paper-scissors is by choosing your strategy at random. Because there are three outcomes —a win, a loss, or a tie—and each strategy has one other strategy that it can beat and one other strategy that can beat it, and we don’t care what strategy we win with, it makes the most sense to pick paper exactly 1/3 of the time, rock 1/3 of the time, and scissors 1/3 of the time. This is called the game’s Nash equilibrium.
While the Nash Equilibrium should be the best strategy in real life, Wang found a decidedly different pattern when he and some other researchers recruited 72 students to play the game. They divided the students into 12 groups of six players and had them each play 300 rounds of rock-paper-scissors against each other. Wang also added a payout in proportion to the number of victories.
Harrison Jacobs
Losing players choose the next strategy in the sequence.
When Wang reviewed the results he found that students chose each strategy close to one third of the time, suggesting the Nash Equilibrium theory. However, when he looked closer, he noticed a more unusual pattern.
The pattern that Wang discovered—winners repeating their strategy and losers moving to the next strategy in the sequence—is called a “conditional response” in game theory. The researchers have theorized that the response may be hard-wired into the brain, a question they intend to investigate with further experiments.
For now, Wang suggests that exploiting the knowledge that most people use the conditional strategy may result in winning a lot more games of rock-paper-scissors.
See Also: The 17 Equations That Changed the Course of History
