In The Simpsons and Their Mathematical Secrets, which comes out today, Simon Singh shows how a series of brilliant Simpsons writers have made the beloved cartoon series smarter about math and science than you ever would have guessed. The following is adapted from the book and published here with the permission of Bloomsbury USA.
Every so often, Homer Simpson explores his inventing talents. In “Pokey Mom” (2001), for instance, he creates Dr. Homer’s Miracle Spine-O-Cylinder, which is essentially a battered trash can with random dents that “perfectly match the contours of the human vertibrains.” But Homer’s inventing exploits reach a peak in “The Wizard of Evergreen Terrace” (1998). The title is a play on the Wizard of Menlo Park, the nickname given to Thomas Edison by a newspaper reporter after he established his main laboratory in Menlo Park, New Jersey. By the time he died in 1931, Edison had 1,093 U.S. patents in his name and had become an inventing legend.
The episode focuses on Homer’s determination to follow in Edison’s footsteps. He constructs various gadgets, ranging from an alarm that beeps every three seconds just to let you know that everything is all right to a shotgun that applies makeup by shooting it directly onto the face. It is during this intense research and development phase that we glimpse Homer standing at a blackboard and scribbling down several mathematical equations.
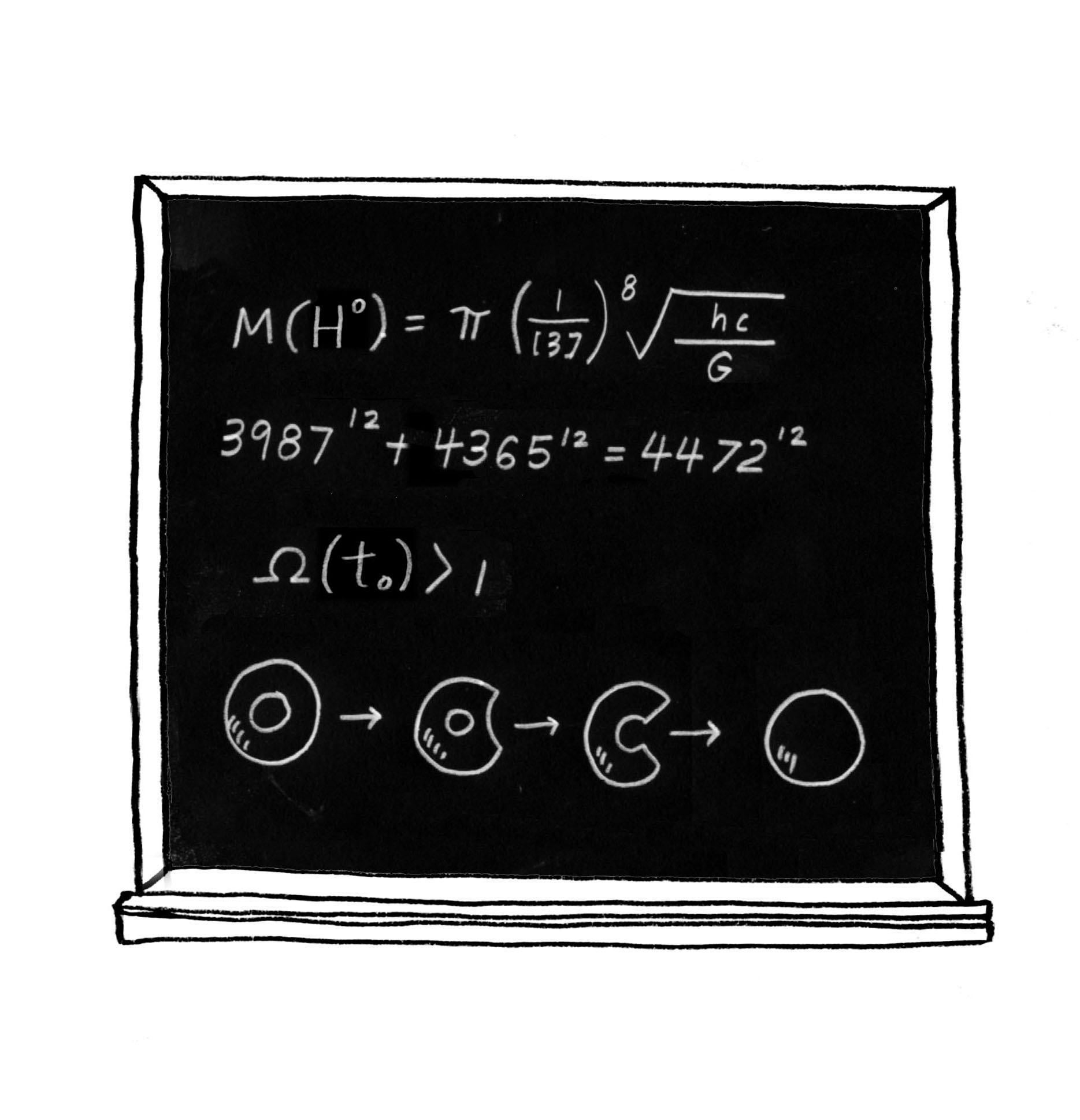
Nicole Gastonguay and Na Kim
The bits of mathematical scribbling on Homer’s blackboard in “The Wizard of Evergreen Terrace” were introduced into the script by David S. Cohen, who was part of a new generation of mathematically minded writers who joined The Simpsons in the mid-1990s. Like Simpsons writers Al Jean and Mike Reiss before him, Cohen had exhibited a genuine talent for mathematics at a young age. At home, he regularly read his father’s copy of Scientific American and toyed with the mathematical puzzles in Martin Gardner’s monthly column. Moreover, at Dwight Morrow High School in Englewood, N.J., he was co-captain of the mathematics team that became state champions in 1984.
At the same time, Cohen maintained an interest in comedy writing and comic books. Even when he went on to study physics at Harvard University, he maintained his interest in writing and joined the Harvard Lampoon, eventually becoming president. Over time, Cohen’s passion for comedy and writing overtook his love of mathematics and physics, and he rejected a career in academia in favor of becoming a writer for The Simpsons. Every so often, however, Cohen returns to his roots by smuggling mathematics into the TV series. The symbols and diagrams on Homer’s blackboard provide a good example of this.
Cohen was keen in this instance to include scientific equations alongside the mathematics, so he contacted one of his high school friends, David Schiminovich, who had stayed on the academic path to become an astronomer at Columbia University. The first equation on the board is largely Schiminovich’s work, and it predicts the mass of the Higgs boson, M(H0), an elementary particle that that was first proposed in 1964. The equation is a playful combination of various fundamental parameters, namely the Planck constant, the gravitational constant, and the speed of light. If you look up these numbers and plug them into the equation, it predicts a mass of 775 giga-electron-volts (GeV), which is substantially higher than the 125 GeV estimate that emerged when the Higgs boson was discovered in 2012. Nevertheless, 775 GeV was not a bad guess, particularly bearing in mind that Homer is an amateur inventor and he performed this calculation 14 years before the physicists at CERN, the European Organization for Nuclear Research, tracked down the elusive particle.
The second equation is … going to be set aside for a moment. It is the most mathematically intriguing line on the board and worth the wait.
The third equation concerns the density of the universe, which has implications for the fate of the universe. If Ω(t0) is bigger than 1, as initially written by Homer, then this implies that the universe will eventually implode under its own weight. In an effort to reflect this cosmic consequence at a local level, there appears to be a minor implosion in Homer’s basement soon after viewers see this equation.
Homer then alters the inequality sign, so the equation changes from Ω(t0) > 1 to Ω(t0) < 1. Cosmologically, the new equation suggests a universe that expands forever, resulting in something akin to an eternal cosmic explosion. The storyline mirrors this new equation, because there is a major explosion in the basement as soon as Homer reverses the inequality sign.
The fourth line on the blackboard is a series of four mathematical diagrams that show a doughnut transforming into a sphere. This line relates to an area of mathematics called topology. In order to understand these diagrams, it is necessary to know that a square and a circle are identical to each other according to the rules of topology. They are considered to be homeomorphic, or topological twins, because a square drawn on a rubber sheet can be transformed into a circle by careful stretching. Indeed, topology is sometimes referred to as “rubber sheet geometry.”
But the second line on Homer’s blackboard is perhaps the most interesting, as it contains the following equation:
3,98712 + 4,36512 = 4,47212
The equation appears to be innocuous at first sight, unless you know something about the history of mathematics, in which case you are about to smash up your slide rule in disgust. For Homer seems to have achieved the impossible and found a solution to the notorious mystery of Fermat’s last theorem!
Pierre de Fermat first proposed this theorem in about 1637. Despite being an amateur who only solved problems in his spare time, Fermat was one of the greatest mathematicians in history. Working in isolation at his home in southern France, his only mathematical companion was a book called Arithmetica, written by Diophantus of Alexandria in the third century a.d. While reading this ancient Greek text, Fermat spotted a section on the following equation:
x 2 + y 2 = z 2
This equation is closely related to the Pythagorean theorem, but Diophantus was not interested in triangles and the lengths of their sides. Instead, he challenged his readers to find whole number solutions to the equation. Fermat was already familiar with the techniques required to find such solutions, and he also knew that the equation has an infinite number of solutions. So, bored with Diophantus’ puzzle, Fermat decided to look at a variant. He wanted to find whole number solutions to this equation:
x 3 + y 3 = z 3
Despite his best efforts, Fermat could only find trivial solutions involving a zero, such as 03 + 73 = 73. When he tried to find more meaningful solutions, the best he could offer was an equation that was out of kilter by just one, such as 63 + 83 = 93 − 1.
Moreover, when Fermat further increased the power to which x, y, and z are raised, his efforts to find a set of solutions were thwarted again and again. Eventually, however, he made a breakthrough. He did not find a set of numbers that fitted one of these equations, but rather he developed an argument that proved that no such solutions existed. He scribbled a pair of tantalizing sentences in Latin in the margin of his copy of Diophantus’s Arithmetica. He began by stating that there are no whole number solutions for any of the infinite number of equations above, and then he confidently added this second sentence: “Cuius rei demonstrationem mirabilem sane detexi, hanc marginis exiguitas non ca- peret.” (“I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.”)
Pierre de Fermat had found a proof, but he did not bother to write it down. This is perhaps the most frustrating note in the history of mathematics, particularly as Fermat took his secret to the grave.
Fermat’s son Clément-Samuel later found his father’s copy of Arithmetica and noticed this intriguing marginal note. He also spotted many similar marginal jottings, because Fermat had a habit of stating that he could prove something remarkable, but rarely wrote down the proof. Clément-Samuel decided to preserve these notes by publishing a new edition of Arithmetica in 1670, which included all his father’s marginal notes next to the original text. This galvanized the mathematical community into finding the missing proofs associated with each claim, and one by one they were able to confirm that Fermat’s claims were correct. Except, nobody could prove that there were no solutions to the equation x n + y n = z n (n > 2).
As each decade passed without a proof, Fermat’s last theorem became even more infamous, and the desire for a proof increased. Indeed, by the end of the 19th century, the problem had caught the imaginations of many people outside of the mathematical community. For example, when the German industrialist Paul Wolfskehl died in 1908, he bequeathed 100,000 marks (equivalent to $1 million today) as a reward for anyone who could prove Fermat’s last theorem. The Wolfskehl Prize catapulted Fermat’s last theorem into public notoriety, and in time it even became part of popular culture. In “The Devil and Simon Flagg,” a short story written by Arthur Porges in 1954, the titular hero makes a Faustian pact with the Devil. Flagg’s only hope of saving his soul is to pose a question that the Devil cannot answer, so he asks for a proof of Fermat’s last theorem.
Fermat’s last theorem has also appeared in novels (The Girl Who Played with Fire by Stieg Larsson), in films (Bedazzled with Brendan Fraser and Elizabeth Hurley), and plays (Arcadia by Tom Stoppard). Perhaps the theorem’s most famous cameo is in a 1989 episode of Star Trek: The Next Generation titled “The Royale,” in which Captain Jean-Luc Picard describes Fermat’s last theorem as “a puzzle we may never solve.” However, Captain Picard was wrong and out of date, because the episode was set in the twenty-fourth century and the theorem was actually proven in 1995 by Andrew Wiles at Princeton University. (Coincidentally, during a brief stint at Harvard University, Wiles lectured Al Jean, who went on to write for The Simpsons.)
When Wiles’ proof was published, it ran to 130 dense pages of mathematics. This is interesting partly because it indicates the mammoth scale of Wiles’s achievement, and partly because his chain of logic is far too sophisticated to have been discovered in the 17th century. Indeed, Wiles had used so many modern tools and techniques that his proof of Fermat’s last theorem cannot be the approach that Fermat had in mind.
This point was alluded to in a 2010 episode of the BBC TV series Doctor Who. In “The Eleventh Hour,” the actor Matt Smith debuts as the regenerated Eleventh Doctor, who must prove his credentials to a group of geniuses in order to persuade them to take his advice and save the world. Just as they are about to reject him, the Doctor says: “But before you do, watch this. Fermat’s theorem. The proof. And I mean the real one. Never been seen before.” In other words, the Doctor is tacitly acknowledging that Wiles’s proof exists, but he rightly does not accept that it is Fermat’s proof, which he considers to be the “real one.” Perhaps the Doctor went back to the 17th century and obtained the proof directly from Fermat.
In “The Wizard of Evergreen Terrace,” Homer appears to have defied the greatest minds across almost four centuries. Fermat, Wiles, and even the Doctor state that Fermat’s equation has no solutions, yet Homer’s blackboard jottings present us with a solution:
3,98712 + 4,36512 = 4,47212
You can check it yourself with a calculator. Raise 3,987 to the 12th power. Add it to 4,365 to the 12th power. Take the 12th root of the result and you get 4,472.
Or at least that is what you get on any calculator that can squeeze only 10 digits onto its display. However, if you have a more accurate calculator, something capable of displaying a dozen or more digits, then you will find a different answer. The actual value for the third term in the equation is closer to
3,98712 + 4,36512 = 4,472.000000007057617187512
So what is going on? Homer’s equation is a so-called near-miss solution to Fermat’s equation, which means that the numbers 3,987, 4,365, and 4,472 very nearly make the equation balance—so much so that the discrepancy is hardly discernible. However, in mathematics you either have a solution or you do not. A near-miss solution is ultimately no solution at all, which means that Fermat’s last theorem remains intact.
David S. Cohen had merely played a mathematical prank on those viewers who were quick enough to spot the equation and clued-up enough to recognize its link with Fermat’s last theorem. By the time this episode aired in 1998, Wiles’ proof had been published for three years, so Cohen was well aware that Fermat’s last theorem had been conquered. He even had a personal link to the proof, because he had attended some lectures by Ken Ribet while he was a graduate student at the University of California, Berkeley, and Ribet had provided Wiles with a pivotal stepping-stone in his proof of Fermat’s last theorem.
Cohen obviously knew that Fermat’s equation had no solutions, but he wanted to pay homage to Pierre de Fermat and Andrew Wiles by creating a solution that was so close to being correct that it would apparently pass the test if checked with only a simple calculator. In order to find his pseudo-solution, he wrote a computer program that would scan through values of x, y, z, and n until it found numbers that almost balanced. Cohen finally settled on 3,98712 + 4,36512 = 4,47212 because the resulting margin of error is minuscule—the left side of the equation is only 0.000000002 percent larger than the right side.
As soon as the episode aired, Cohen patrolled the online message boards to see if anybody had noticed his prank. He eventually spotted a posting that read: “I know this would seem to disprove Fermat’s last theorem, but I typed it in my calculator and it worked. What in the world is going on here?”
He was delighted that budding mathematicians around the world might be intrigued by his mathematical paradox: “I was so happy, because my goal was to get enough accuracy so that people’s calculators would tell them the equation worked.”
Cohen is very proud of his blackboard in “The Wizard of Evergreen Terrace.” In fact, he derives immense satisfaction from all the mathematical tidbits he has introduced into The Simpsons over the years: “I feel great about it. It’s very easy working in television to not feel good about what you do on the grounds that you’re causing the collapse of society. So, when we get the opportunity to raise the level of discussion—particularly to glorify mathematics—it cancels out those days when I’ve been writing those bodily function jokes.”
Reprinted from The Simpsons and their Mathematical Secrets by Simon Singh. Copyright © 2013 by Simon Singh. Used with permission of Bloomsbury USA.
