Why does time flow from the past to the future?
That’s an extraordinarily deceptively simple question. It seems so, well, straightforward. But when you start to really investigate it, you wind up going down a rabbit hole of twisty, complicated physics.
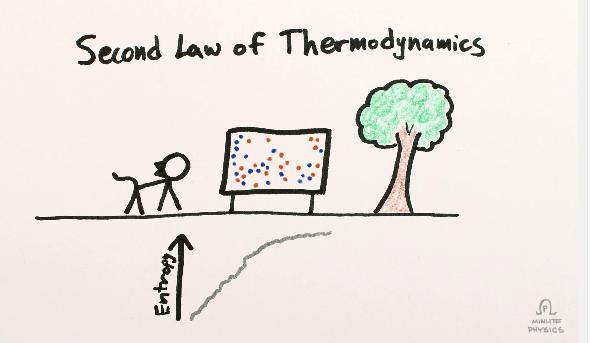
When I first started reading about this, I was surprised to learn that it’s tied to entropy. That’s a concept in physics that has a lot of different ways to think about it, but the most common colloquially is to say it’s the degree of disorder in a system. The pieces in a completed jigsaw puzzle are highly ordered, but those same pieces when you first open the box are highly disordered. So the latter has higher entropy.
What does this have to do with time? My friend Sean Carroll—a cosmologist who spends his time thinking about, um, time—and Henry Reich, who draws Minute Physics, collaborated on a series of videos explaining this. As I write this article the first two are out, and they’re intriguing. Here’s the first one:
I can’t wait to see the rest! They’ll be out soon. In the meantime, Sean has books on this topic: From Eternity to Here, which is excellent, and The Big Picture, which I am currently reading right now. It’s also very, very good.
I’ve always struggled with the concept of things like entropy, time, and Boltzmann Brains. Talking with Sean has helped, but reading his books and watching those videos will go a long way, too. It’s amazing to me, as he explains in the video, that the second law of thermodynamics is the only (or one of the only) basic macroscopic physics equations that has time in it explicitly as moving from past to future. Why? Entropy.
It’s like dealing out a hand of five playing cards. There are roughly 2.6 million different hands you could get this way. But only a handful of them have what we would think of as value. A straight, for example, or a flush. If you get 2 3 4 5 6 of hearts, that’s a straight flush, and is extremely ordered. That means it has very low entropy.
Another hand, like 3 6 8 J K, with different suits, is not ordered at all. It has high entropy. Those high entropy, unordered hands are far more common than low entropy, ordered hands. That’s why we value the latter. The odds of getting a straight flush in five card stud are about 1 in 72,000, but 50 percent of the time you won’t even get a pair.
So if you shuffle the cards and deal them, you are far more likely to get a disordered high-entropy hand than an ordered, low-entropy one. That’s why they call it gambling.
Henry Reich
Another way to look at it is to imagine a container full of gas. On the molecular level, the molecules of gas are distributed more or less randomly. If you swap two molecules with each other the gas looks pretty much the same, and that’s also true if you move a molecule a little bit, say, to the left or right. The number of different ways you could swap or move molecules without changing the nature of the gas is immense, which means it’s incredibly high entropy. If you cool the gas so much it becomes a liquid, or a solid, there are far fewer states each molecule can occupy, so the entropy, the state of disorder, is lower.
If you sit around and watch that gas for a bazillion years, chances are it will always look pretty much the same, even as the molecules move around. The chance of them suddenly liquifying, or all moving to the left side of the container, is extremely small. High entropy states are hugely more likely than low ones. And if you find yourself in a low-entropy state, after a moment the odds are you’ll be back in some high-entropy one.
That’s what Sean and Henry are outlining in those videos. We’re in a relatively low entropy Universe right now. We see it expanding, we see stars dying, we know eventually matter and energy will be more randomly distributed. We’re moving toward a higher entropy Universe, which strongly implies that it was lower entropy in the past. That’s the Big Bang.
Eventually, the Universe will become so disordered that entropy will be maximized. At that point, time has little or no meaning. After all, if you move stuff around and it looks exactly the same, how do you measure time? Time is a measure of the change in events. If everything is the same, time has nothing to measure.
Mind you, I’m still exploring all these concepts, and I’m no expert. But maybe, after watching those videos and reading this, you’ll get a taste of just how deep this runs. It goes straight to the heart of our most basic philosophies, of some of the biggest questions we can ask. Why is there something rather than nothing? Why is that something—the Universe itself—the way it is, and not some different way? Why does time exist, and why does it flow into the future? Why don’t we remember the future and predict the past?
These are heady questions, and I’m thankful that there are people like Sean trying to figure them out, and people like Henry helping the rest of us come along for the ride. It’ll be interesting to see where this goes. Or where it went. Either way.
