That high-pitched noise you may be hearing emanating from your computer speakers is the combined sonic eruption of millions of nerds squeeing, for today is Pi Day.
Or π Day, if you prefer the original Greek. Either way, here in the states we reckon the date as 3/14, March 14, which are the first three digits of the mathematical constant. Last year I wrote a fun discussion of this number, why it’s so useful, and where it pops up in the world of math and science.
There is one quirk I forgot to add back then: There are very close to π x 10,000,000 seconds in a year. That’s accurate to better than half a percent! A coincidence, but a cool one.
But I have not come here to praise π, though neither am I here to bury it. But there are folks who think it should be. Buried, I mean. Or better, replaced with a different number: τ. That is, the Greek letter tau, which represents a number they claim is better: 2 x π, or 6.283185307…
At first blush, this may seem marginally sacrilegious. Replace π? Never!
However, the Tauists (if I may call them that) are pretty serious about this. I’ve heard about it for years, but someone mentioned it to me the other day and got me thinking more about it. If you wish, there is a website devoted to it that’s worth a look, and the Tau Manifesto (yes, seriously) is an interesting read (though there is some intense math there; fairly warned be thee, says I).
I do agree with some of what’s said there. The best point made has to do with why we all know π in the first place: the circumference of a circle. Mathematically, the circumference (the length around a circle) is equal to 2 x π x the radius (usually written as 2 π r).
Where this gets interesting is when you deal with radians (usually taught in high-school math). Instead of measuring the size of an angle in degrees, you can measure it in terms of the whole circumference (360°) of the circle. That’s equal to 2 π, so 180° (halfway around the circle)= π radians, 90° = ½ π, and so on. These units are pretty useful in astronomy and other fields. They’re called radians because they’re based on the radius of the circle (assumed to be equal to 1, making it unitless).
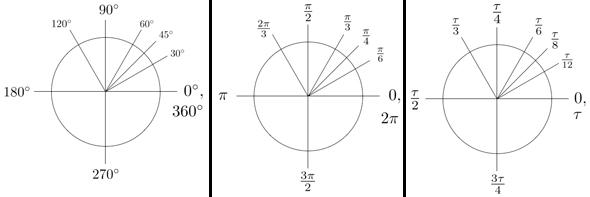
Illustrations by Michael Hartl from the Tau Day website
Replacing π with τ makes sense, in this case. Then 360° = τ, 180 = ½ τ, 90° = ¼ τ … and intuitively, this works better. A whole circle is one τ, a half circle is half τ, etc. τ becomes a measure of the rotation of a circle, a single turn if you will, which is easier to literally grasp with our monkey brains, accustomed as we are to physically moving things with our hands. I rather like this.
The Tauist argument gets weaker to me though when you get past the circumference and look at the area. That’s equal to π r2. So in terms of τ it’s ½ τ r2, and we’re right back to clunky units. It’s the same for a sphere. The surface area is 4 π r2, or in τ units 2 τ r2. That’s no better or worse. The volume of a sphere is 4/3 π r3, which becomes 2/3 τ r3, which again is not really any better.
So in one case—using radians—sure, τ works out better than π. But in most other cases it’s a bit of a wash.
And I’d take that even further: In the end (except for that concept of one turn per τ) it’s all just a matter of what constant you’re using; 2 instead of 4, 1 instead of 2, whatever. In the very advanced cases of integrals, statistics, and such, you’re really just replacing one number with another. There are some conceptual advantages, but would they outweigh having to revamp such an ingrained system? If you’re learning how to calculate standard deviations from a dataset or how to do integrals in the complex plane, I’d wager the difference between π and τ isn’t too hard a concept to master.
Photo bu AmitP on Flickr, modified slightly by Phil Plait
Now, don’t get me wrong: If we could do it all over again, go back in time to the first person to use π and talk them out of it, then, yeah, I think using τ would be better. If it’s arbitrary in the vast majority of cases and makes understanding radians easier for high-school students, then sure! Fine by me.
But in reality, we can’t do that. π is everywhere already, and it works pretty well.
And that’s why I don’t think this idea will ever really catch on. If we can’t get this country to go metric, for crying out loud (and mind you, this is coming from your über-metric host, who thinks we should use Kelvin over Celsius and prefers centimeters to meters), then rebooting the use of a fundamental constant is utterly hopeless … especially when the Internet is in love with the number we have now.
If you’re into math as a system of understanding and as having fun concepts to play with, then I highly recommend reading about τ. It’s interesting, and there may be some stuff there you didn’t know (which was true for me). But in the end, it won’t stop me from using π and celebrating March 14 every year.
And hey, let’s let bygones be bygones: We can celebrate June 28, too.
(Note: I would think that if you are the kind of person concerned about τ versus π, then you might be equally concerned over the dumb way we Americans write dates: Month/Day/Year, which is mixed up. It makes way more sense to go from small to big units: Day/Month/Year. But if we do, π Day disappears! 3/14 would be the third day of the 14th month, which raises obvious problems.)
