Of the Algorithms, by the Algorithms, for the Algorithms
Can a bunch of mathematicians make government more representative?
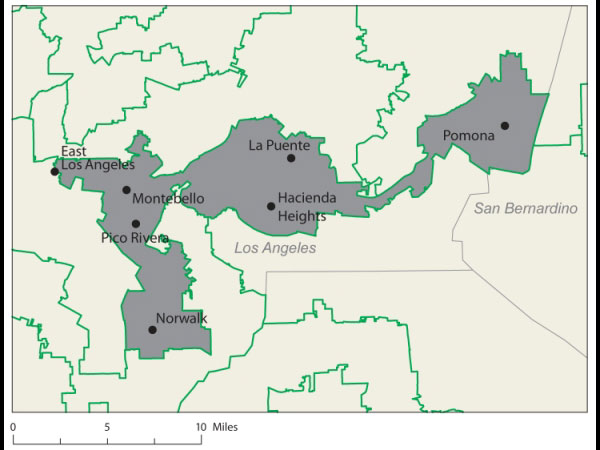
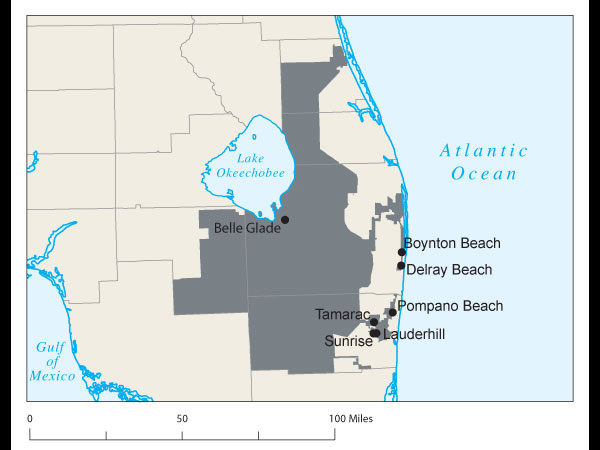
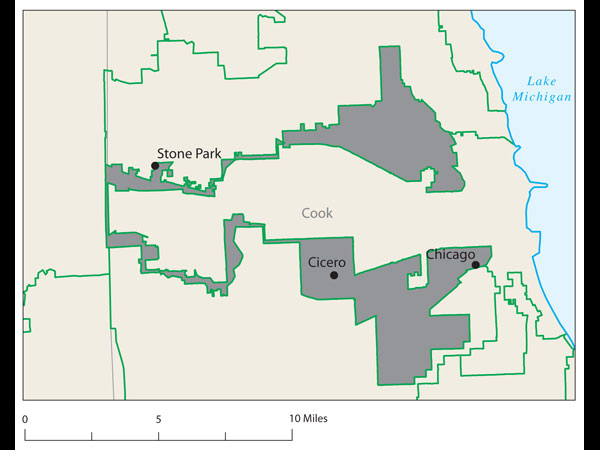
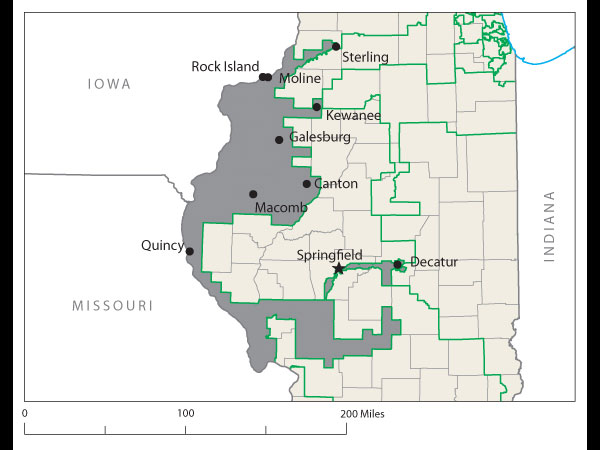
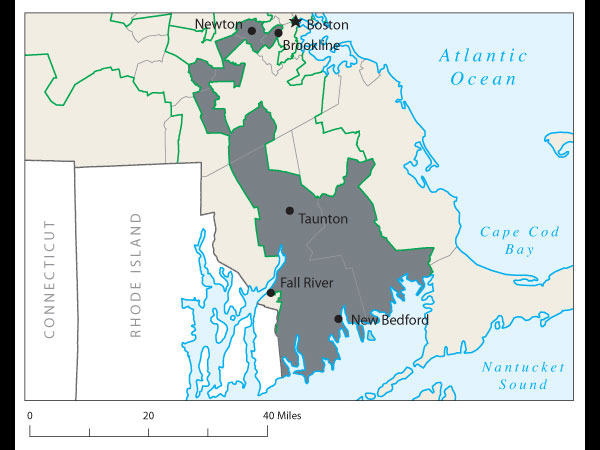
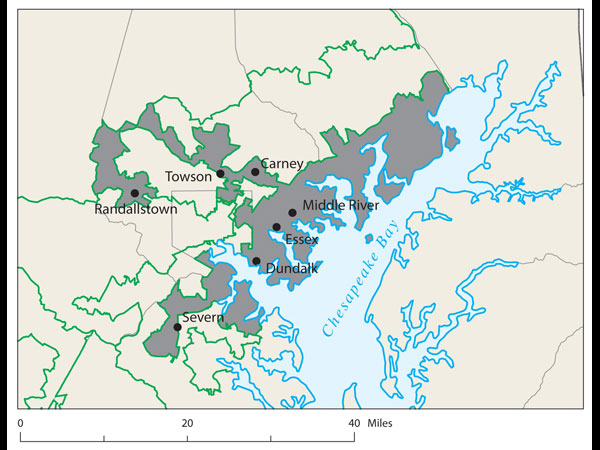
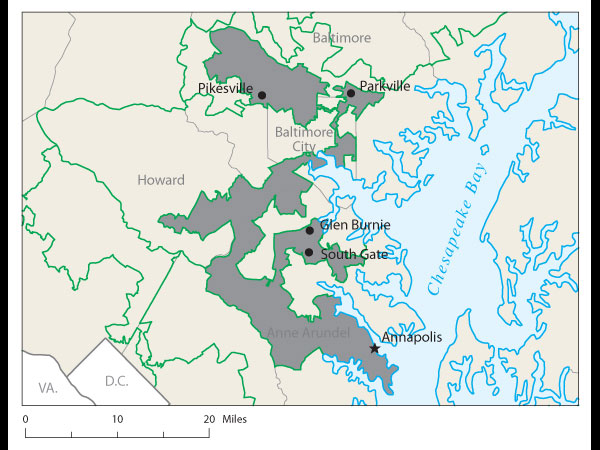
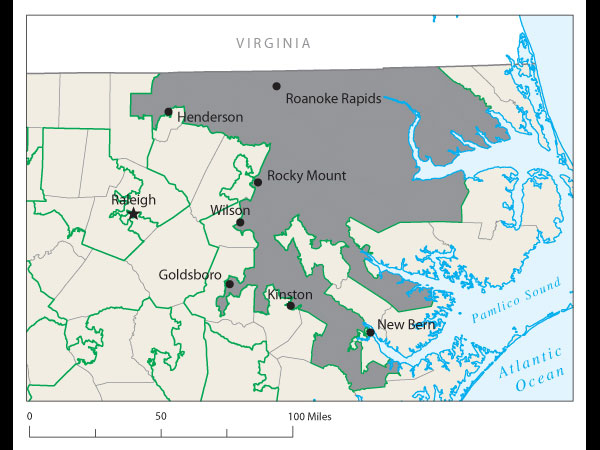
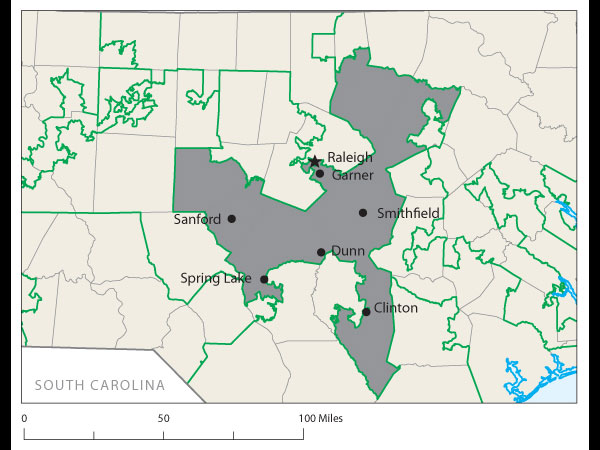
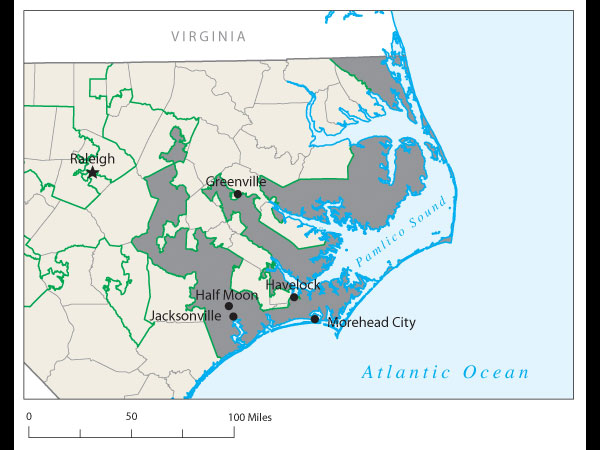
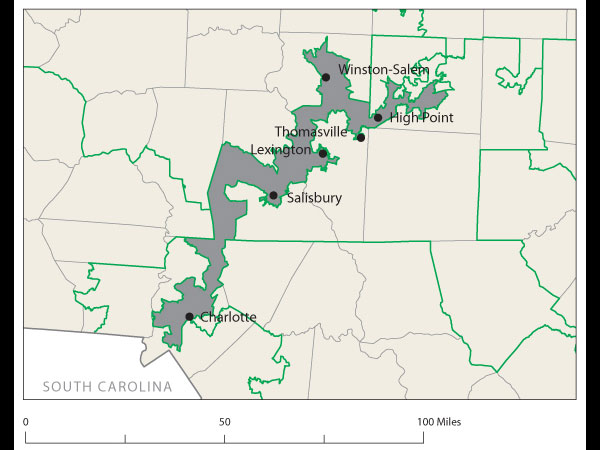
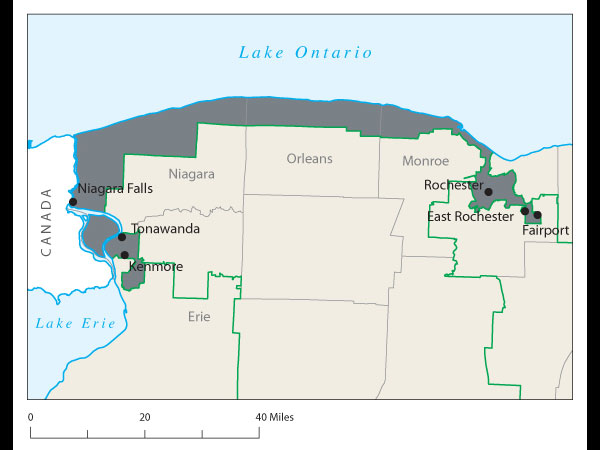
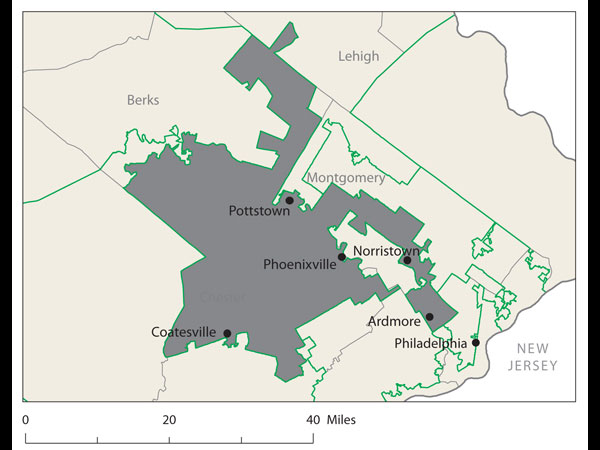
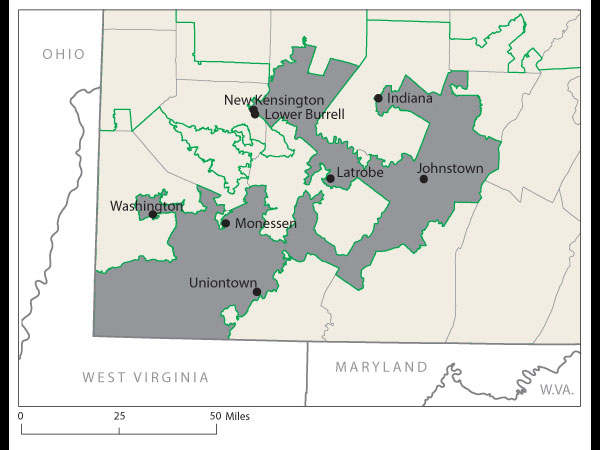
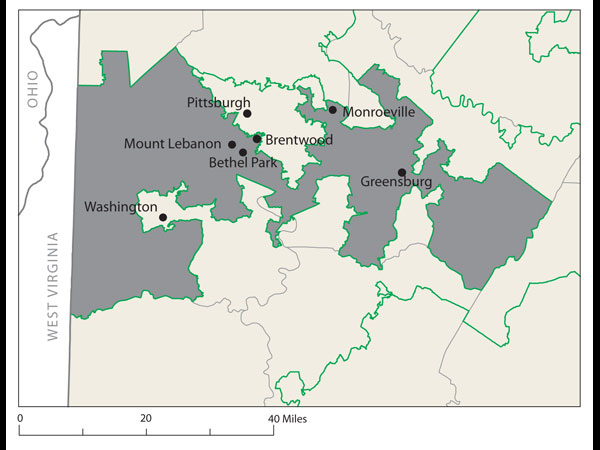
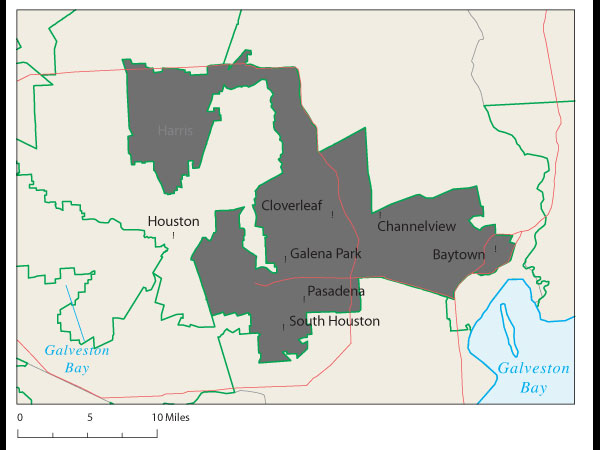
Proof came at a recent joint meeting of the two major American mathematical societies during an afternoon session on ways to use math in the battle against gerrymandering. One audience member argued stridently that Florida's 23rd Congressional District, with its decrepit appendage along the coastline, was the weirdest. Later, that got trumped by Wisconsin's 61st state assembly district, which is split into three pieces. Then again, there's Pennsylvania 12th Congressional, home to John Murtha, which looks like an anchor glued to a sea anemone.
For decades, math and computer science have played a profound role in the drawing of legislative districts. And it's hard to argue that they've improved the process. As the amount of information and computing power available to the gerrymanderers has ballooned, they have gotten much better at surgically crafting districts to their precise desires.
So, with a reapportionment of House seats coming up in just over two years, after the next decennial census, mathematicians are now plotting their revenge. After 2010, most states will redraw their congressional districts to account for population shift, sometimes adding or subtracting seats. It's tough to find many defenders of the status quo, in which a supermajority of House seats are noncompetitive. (Congressional Quarterly ranked 324 of the 435 seats as "safe" for one party or the other in 2008.) The mathematicians—and social scientists and lawyers—who gathered to discuss the subject Thursday are certain there's a better way to do it. They just haven't quite figured out what it is.
In theory, it makes wonderful sense to hire an algorithm to do the job. Simply plug in all the requirements for a congressional district—relatively equal population, compliance with the Voting Rights Act, and so forth—and let the nonpartisan processor divvy up the state into sensible, shapely chunks. Algorithms, after all—thanks in part to Google—are having a great decade. In other areas where there's a tremendous mess of disorganized, disparate data, like the Internet or the news, we're quite comfortable letting a series of calculations determine which ones are the most important or interesting.
So, why is an algorithmic solution for congressional redistricting such a pipe dream?
In part it's because it is surprisingly hard to define, or at least reduce to a set of rules, what a "gerrymandered district" is. Writing a formula for drawing districts requires us to define how funny-looking is too funny looking. And what is funny, anyway?
"The idea is that circles are the best shape for districts," said George Washington University's Daniel Ullman, talking about one school of thought. "Unfortunately, they don't tessellate well." This was apparently a joke, because the room burst out laughing. For the rest of the afternoon, the word tessellate never failed to produce giggles. (Tessellate means to tile together, as in an M.C. Escher drawing.)
There are more than 30 ways to look at the shape of a district and put a number on how screwed up it is. Many practitioners, for example, have treated the district like a free-standing puzzle piece, finding the center of gravity and calculating the square of the distance of each point from that center—what's known as the moment of inertia in physics. The lower the score, the better; districts that are long and dispersed will have many points far from the center of gravity, while compact districts will have fewer. (There are variations on this method, like summing the squares of the distances between individual people in the district. This way, a district isn't penalized for vast swaths of unpopulated area.)
These calculations are usually grouped under the idea of "compactness" of a district, which has found its way into many state regulations. The most interesting proposal of the afternoon came from a Caltech grad student named Alan Miller, who proposed a simple test: If you take two random people in a district, what are the odds that one can walk in a straight line to the other without ever leaving the district? (Actually, it's without leaving the district while remaining in the state, so as not to penalize districts like Maryland's 6th, which has to account for Virginia's hump.) This rewards neat, simple shapes. But it penalizes districts like Maryland's 3rd, which looks like something out of Kandinsky's Improvisation 31.
Miller's point is that, by just about any measure of "compactness," one can imagine highly gerrymandered districts that still score pretty well. He and his co-authors prefer the term bizarreness for his measurement. Basically, it's an easily quantifiable standard that could contain gerrymandering without punishing legitimate districts that are funny-looking by necessity.
Still, how much does the shape of a district really tell us about the degree of political monkey business? If a district has to take a few odd turns to encompass a diverse, competitive group of voters, is that a bad thing?
Part of the difficulty of this debate is that no one can agree on the definition of a "perfect distribution"—that is, what the demographics of a district's population should be. Should they match the demographics of the whole state? Probably not; this would require slicing up urban areas like a pizza into different districts and would award a highly disproportionate number of seats to the majority party in the state. But the goal isn't necessarily to have the distribution of seats match the distribution of Democrats and Republicans in the state. If that were the idea, we could just hold elections the way many European countries do it. (One of the presenters said he gave a similar talk in Bulgaria, where the audience was totally perplexed at how complicated we make it here.)
The best idea of the session, which was arranged by Scientists & Engineers for America, came from Sam Hirsch, who is not a mathematician but a lawyer. He thinks redistricting should be a public contest that uses the law and the metrics developed by mathematicians as a scoring system. It's kind of like a Netflix Prize for redistricting.
Under the Hirsch plan, any public proposal would have to comply with the law and current standards for equal population, continuity, and so forth. For all the plans that passed this threshold, there would be three further metrics:
- County integrity (matching district lines with county lines when possible);
- Partisan fairness (roughly half the districts should be more Democratic than the state as a whole, while the other have should be more Republican—the system doesn't include third parties);
- Competitiveness (a little more complicated, but recalculating previous election data according to the new districts).
The advantage of a plan like Hirsch's, which draws heavily on a lot of the mathematicians' research, is that it's quantifiable. Once plans start rolling in, any future proposal would have to score higher on those three metrics to be considered. And it would be fairly easy to substitute metrics if a particular state wanted, say, to value compactness (or nonbizarreness) over county integrity.
Hirsch is realistic about the odds that many states would adopt his plan wholesale (though his plan includes a sample constitutional amendment just in case), and it would take years for today's computers even to run the numbers on every possible plan. But the basic idea that districts can be rigorously quantified as to their competitiveness, bizarreness, congruity with media markets, racial enfranchisement—or any number of other metrics—is a potent one. Once plans can be evaluated according to measures that everyone can agree with, at least in principle, one needs only some form of competition to find the one that satisfies all parties reasonably equally. Screw the algorithms: Let the people do the heavy lifting.
Like Slate on Facebook. Follow us on Twitter.