Excerpted from Single Digits: In Praise of Small Numbers by Marc Chamberland. Out now from Princeton University Press.
What do grocers and honeybees have in common? The obvious answer is that they are both adept at providing food for others. But there is a richer, more technical answer to this question: These two groups know how to efficiently pack their resources.
Honeycombs, made from the wax secreted by bees, are used to store honey, pollen, and larvae. For thousands of years, the honeycomb’s hexagonal structure has been noted and admired. It is wondered whether this entomological architecture inspired the interior ribbing and hidden chambers in the dome of the Pantheon in Rome. Today honeycomb structures have numerous engineering and scientific applications, including in the aerospace industry.
Why do honeycombs have a hexagonal structure? Pappus of Alexandria declared that bees “possessed a divine sense of symmetry,” and Charles Darwin described the honeycomb as a masterpiece of engineering that is “absolutely perfect in economizing labor and wax.” A mathematical rationale was given by the Polish polymath Jan Brożek (1585–1652): The hexagon tiles the plane with minimal boundary. Stated another way, Brożek conjectured that the optimal way to cover a large region with shapes of the same area while minimizing the boundary is to use the hexagonal structure. This problem resisted a solution for centuries but was finally positively settled by Thomas Hales in 1998.

Photo by José Luis Sánchez Mesa/Flickr Creative Commons
Conveniently, the mathematical tools Hales used to prove the Honeycomb Conjecture were recycled after having settled another long-standing open problem, Kepler’s Conjecture. Sometimes called the Cannonball Problem, it asks whether the traditional pattern used to stack oranges (or cannonballs) is optimal. Specifically, the arrangement of equal-sized spheres to fill a space with the minimum amount of wasted volume is the so-called close packing, which consists of layers of spheres whose centers form a hexagonal lattice. If equal-sized balls are dropped into a large container at random, experiments suggest that the density—the proportion of the container’s volume filled by balls—is roughly 65 percent. The hexagonal close-packing arrangement yields an average density of π/(3√2) ≈ 74 percent. Efficient packing is the name of the game. This problem attracted the attention of mathematical giants such as Carl Gauss, who proved a special case. In 1900, David Hilbert’s address at the International Congress of Mathematics in Paris described 10 problems that he felt would strongly influence the direction of mathematical research in the 20th century. The print version of his address includes 23 problems. Kepler’s Conjecture is part of Hilbert’s Problem 18.
Like the Honeycomb Conjecture, the Kepler Conjecture languished for centuries until a solution was provided by Hales. In 1953 the Hungarian mathematician László Fejes Tóth showed that the problem could be reduced to a finite (but very large) number of cases. He also grasped that such a challenge could be met with a computer, but this dream could not be realized at the time. Hales, assisted by his graduate student Samuel Ferguson, transformed the situation into minimizing a function of 150 variables. He showed that if the minimum of this function for 5,000 different configurations was larger than the minimum value obtained for the close packing, then the problem was solved. The solution involved a monstrous amount of computing, roughly 100,000 linear programming problems, an area of applied mathematics that is foundational to resource management. It took Hales several years to complete this project and settle the claim of Kepler’s Conjecture.
The solution attracted some controversy. The editors of the prestigious journal Annals of Mathematics agreed to publish it pending approval of a referee panel. After four years of work, the head of the panel, Gábor Fejes Tóth (son of László Fejes Tóth), reported that the panel was “99% certain” of the correctness of the proof but reserved claiming complete assurance because computer calculations could not be verified. While the mathematical community has generally accepted the proof, Hales has pursued a formal proof by using automated proof-checking software. In 2014 this project was announced to be complete.
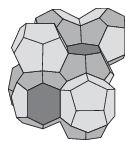
Image courtesy Princeton University Press
Another packing problem is the Kelvin Conjecture. This is the three-dimensional version of the Honeycomb Conjecture, asking for the arrangement of three-dimensional cells of equal volume that minimizes the surface area between the cells. Lord Kelvin postulated that the solution consisted of filling the space with tetradecahedrons, polyhedrons with six square faces and eight hexagonal faces. Given the success of the Honeycomb and Kepler conjectures, one might be forgiven in quickly asserting that Kelvin’s Conjecture must also hold. But wishful thinking is not sufficient. In 1993, Irish physicist Denis Weaire and his student Robert Phelan used computer simulations to find a more efficient cell that tiles three-dimensional space. This involves two different polyhedra with the same volume: an irregular dodecahedron with pentagonal faces, possessing tetrahedral symmetry, and a tetrakaidecahedron, which has two hexagonal and 12 pentagonal faces possessing antiprismatic symmetry. This configuration has 0.3 percent less surface area than the arrangement asserted in the Kelvin structure, but it is unknown whether this is optimal.

Photo by Charlie Fong courtesy Wikimedia Commons
The Weaire–Phelan structure is found in some crystal structures. Gas hydrates formed by methane, propane, and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Weaire–Phelan structure. For a different application, this structure, like the honeycomb structure in two dimensions, is observed to be naturally strong. The Weaire–Phelan structure inspired the design of the Beijing National Aquatics Center—aka the Water Cube—for the 2008 Olympics.
Excerpted from Single Digits: In Praise of Small Numbers by Marc Chamberland © 2014 by Princeton University Press. Reprinted by permission.
