Depressed people send more email. They spend more time on Gchat. Researchers at the Missouri University of Science and Technology recently assessed some college students for signs of melancholia then tracked their behavior online. “We identified several features of Internet usage that correlated with depression,” they said. Sad people use IM and file-share. They play video games. They surf the Web in their own, sad way.
Not everyone found the news believable. “Facepalm. Correlation doesn’t imply causation,” wrote one unhappy Internet user. “That’s pretty much how I read this too… correlation is NOT causation,” agreed a Huffington Post superuser, seemingly distraught. “I was surprised not to find a discussion of correlation vs. causation,” cried someone at Hacker News. “Correlation does not mean causation,” a reader moaned at Slashdot. “There are so many variables here that it isn’t funny.”
And thus a deeper correlation was revealed, a link more telling than any that the Missouri team had shown. I mean the affinity between the online commenter and his favorite phrase—the statistical cliché that closes threads and ends debates, the freshman platitude turned final shutdown. “Repeat after me,” a poster types into his window, and then he sighs, and then he types out his sigh, s-i-g-h, into the comment for good measure. Does he have to write it on the blackboard? Correlation does not imply causation. Your hype is busted. Your study debunked. End of conversation. Thank you and good night.
The correlation phrase has become so common and so irritating that a minor backlash has now ensued against the rhetoric if not the concept. No, correlation does not imply causation, but it sure as hell provides a hint. Does email make a man depressed? Does sadness make a man send email? Or is something else again to blame for both? A correlation can’t tell one from the other; in that sense it’s inadequate. Still, if it can frame the question, then our observation sets us down the path toward thinking through the workings of reality, so we might learn new ways to tweak them. It helps us go from seeing things to changing them.
So how did a stats-class admonition become so misused and so widespread? What made this simple caveat—a warning not to fall too hard for correlation coefficients—into a coup de grace for second-rate debates? A survey shows the slogan to be a computer-age phenomenon, one that spread through print culture starting in the 1960s and then redoubled its frequency with the advent of the Internet. The graph below plots three common versions of the phrase going back to 1880 as they turn up in Google Books. It’s that right-most rise that interests me—the explosion of correlations that don’t imply causation in the 1990s and 2000s. Beware of spurious correlations, I know! But it is tempting to say the warning spread in the squall of data on the Web, as a means of warding off the cheap associations that ride a stormy sea of numbers. If now we’re quick to say that correlation is not causation, it’s because the correlations are all around us.
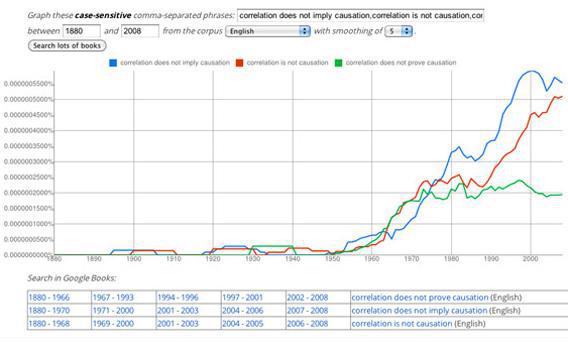
Courtesy Google.
Let’s go back a little further, though, to the origins of the phrase itself. Those first, modest peaks of “correlation is not causation” show up in print in the 1890s—a date that happens to coincide with the discovery of correlation itself. That’s when the British statistician Karl Pearson introduced a powerful idea in math: that a relationship between two variables could be characterized according to its strength and expressed in numbers. Francis Galton had futzed around with correlations some years before, and a French naval officer named Auguste Bravais sketched out some relevant equations. But it was Pearson who gave the correlation its modern form and mathematics. He defined its role in science.
Philosophers had spent centuries, by that point, on the question of how the mere association of events might reveal their causal links and what it means to say that one thing can ever cause another. The ambiguity of correlations was well-known. Victorian logician Alexander Bain wasn’t breaking new ground in 1870 when he warned his readers of the “fallacy of causation,” whereby we might assume that, say, “the healthy effect of residence at a medicinal spa is attributed exclusively to the operation of the waters,” as opposed to being caused by “the whole circumstances and situation.” The confusion between correlation and causation, he said (not quite using the famous phrase), “prevails in all the complicated sciences, as Politics and Medicine.”
With the arrival of Pearson’s coefficients and the transformation of statistics, that “fallacy” became more central to debate. Should scientists even bother with a slippery concept like causation, which can’t truly be measured in the lab and doesn’t have a proper definition? Maybe not. Pearson’s work suggested that causation might be irrelevant to science and that it could in certain ways be indistinguishable from perfect correlation. “The higher the correlation, the more certainly we can predict from one member what the value of the associated member will be,” he wrote in one of his major works, The Grammar of Science. “This is the transition of correlation into causation.”
But Pearson’s language on the matter was inconsistent and confusing. The father of correlation did worry about its overuse, says Theodore Porter, a historian of science at UCLA and a Pearson specialist. A footnote to the second edition of The Grammar of Science, published in 1900, lays out a critique of spurious relationships in terms that would not look out of place on an Internet message board:
All causation as we have defined it is correlation, but the converse is not necessarily true, i.e. where we find correlation we cannot always predict causation. In a mixed African population of Kaffirs and Europeans, the former may be more subject to smallpox, yet it would be useless to assert darkness of skin (and not absence of vaccination) as a cause.
Pearson’s critics expressed the same concern. That year in Science, a reviewer called out the book’s “transition of correlation into causation” as one that is “scarcely allowable” and went on to note (emphasis mine) that, “correlation does not imply causation, though the converse is no doubt true enough.”
So it seems the fear of correlations was formalized—made into a turn of phrase, I mean—at around the time that correlations came into formal being. One might say (citing another correlation) that Pearson’s work marks the transition from an age of causal links to one of mere relationships—from anecdotal science to applied statistics. As correlations split and multiplied, we needed to remind ourselves of what they meant and what they didn’t. The graph below, again from Google Books, shows the shift in language that marked this change in spirit: Up until the early 1900s, causation showed up more often than correlation in the corpus; then the concepts flip. (I’ll let someone else explain why correlations have been trending downward since 1976.)
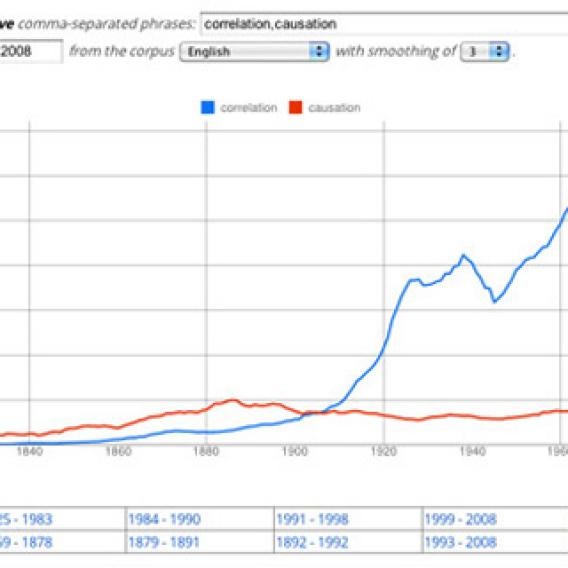
Courtesy Google.
In the decades to come, the phrase correlation does not imply causation made its way into textbooks and academic journals, while the social sciences were made over with newfangled statistics. By the 1940s, economists had devised a name for the insufficiency of correlations: They called it the “identification problem.” A flood of numbers in the postwar years may have made the anxiety more acute until its apotheosis in the present day, when Google, Amazon, and the other data juggernauts belch smoggy clouds of information and spit out correlations by the ton. “That may be as deep a sense of causation as they care about,” Porter says. “To them, perhaps, automated number-crunching stands for the highest form of knowledge that civilization has ever produced.” In that sense, the admonitory slogan about correlation and causation isn’t so much a comment posted on the Internet as a comment posted about the Internet. It’s a tiny fist raised in protest against Big Data.
But there’s still another puzzle in the phrase. To say that correlation does not imply causation makes an important point about the limits of statistics, but there are other limits, too, and ones that scientists ignore with far more frequency. In The Cult of Statistical Significance, the economists Deirdre McCloskey and Stephen Ziliak cite one of these and make an impassioned, book-length argument against the arbitrary cutoff that decides which experimental findings count and which ones don’t. By convention, we call an effect “significant” if the chances of its deriving from a twist of fate—as opposed to some more genuine relationship—are less than 5 percent. But as McCloskey and Ziliak (and many others) point out, there’s nothing special about that number and no reason to invest it with our faith.
It’s easy to imagine how this point might be infused into the wisdom of the Web: “Facepalm. How many times do I have to remind you? Don’t confuse statistical and substantive significance!” That comment-ready slogan would be just as much a conversation-stopper as correlation does not imply causation, yet people rarely say it. The spurious correlation stands apart from all the other foibles of statistics. It’s the only one that’s gone mainstream. Why?
I wonder if it has to do with what the foible represents. When we mistake correlation for causation, we find a cause that isn’t there. Once upon a time, perhaps, these sorts of errors—false positives—were not so bad at all. If you ate a berry and got sick, you’d have been wise to imbue your data with some meaning. (Better safe than sorry.) Same goes for a red-hot coal: one touch and you’ve got all the correlations that you need. When the world is strange and scary, when nature bullies and confounds us, it’s far worse to miss a link than it is to make one up. A false negative yields the greatest risk.
Now conditions are reversed. We’re the bullies over nature and less afraid of poison berries. When we make a claim about causation, it’s not so we can hide out from the world but so we can intervene in it. A false positive means approving drugs that have no effect, or imposing regulations that make no difference, or wasting money in schemes to limit unemployment. As science grows more powerful and government more technocratic, the stakes of correlation—of counterfeit relationships and bogus findings—grow ever larger. The false positive is now more onerous than it’s ever been. And all we have to fight it is a catchphrase.
